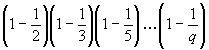Testing Robinson numbers for primality

The reader is assumed to be familiar with searches for Proth primes and related forms using software such as Proth.exe, Newpgen.exe, Primeform.exe, Prp.exe, Winbitwin.exe, Titanix,exe, etc.

There are a number of ways of testing a positive integer p for primality. These include :

1. a full sieve to the root of p;
2. variations of the p- 1 methods developed by Brillhart, Morrison and Selfridge, based on earlier results by Lucas, Proth and Pocklington, wherein p- 1 is factored completely or partially and the factors used to test for pseudoprimality.
3. variations of the p+1 methods developed by Brillhart, Morrison and Selfridge from earlier ideas by Lucas and Lehmer.
4. combinations of both of the previous methods.
5. generic primality testing algorithms such as ECPP (Elliptic Curve Primality Proving), by Atkin and Morain (Titanix.exe is an implementation of this), and APR-CL (Adleman, Pomerance, Rumely, Cohen , Lenstra).

In practice, whether for finding Proth primes, primes in arithmetic progression, Cunningham chains, etc., interest will usually be in searching across large ranges of numbers of the form k*2ⁿ +1, where the p- 1 Proth test can be used. The initial search space (i.e. the entire set of numbers to be considered) is substantially restricted by using a partial sieve to a manageable limit, as it done by both Proth.exe and Newpgen.exe. These programs can be used to build lists of combinations k & n which may then be tested for pseudoprimality using Prp.exe and then primality using Proth.exe or Primeform.exe. Note that the generic algorithms are not equipped to cope with numbers of the sizes typically considered here.

I am interested in the typical number of pseudoprimality / primality tests that have to be carried out across a close range (I mean by this that values of n are approximately equal) in order to locate a prime. In particular, in searching for Keller primes, I am interested in testing a fixed and limited number of k values over given n ranges. Since Newpgen.exe is not suited to this, the alternative is to generate quickly an initial test set using a very brief sieve and then passing the output of this to Proth.exe, using the "Factors only" preference and with a fixed manual sieve limit. The idea of a fixed limit sieve is important in what follows.

Now for some theory : It is widely known (and I won't give references) that p (x), the number of primes less than or equal to x, is approximately equal to and that the likelihood that x is prime is approximately . But what if x (or p, since we are interested in primes) has already survived a sieve to a limit q ? Now, it is obvious that the proportion of integers surviving a sieve to q is s(q) = 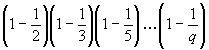. If p has survived a sieve to q, then the likelihood that p is a prime is therefore , or where t(q) = , and the expected number of tests required in order to obtain a prime is the inverse of this. A classical result by Mertens implies that t(q) ® eg .log(q) as q ® ¥ , where g is Euler's constant, and so the value of t(q) rises logarithmically. The two tables below comparative values between the calculated value and the estimated value for a variety of key limits.

and

Consider p = k*2ⁿ + 1. Then log (p) » n*log(2) + log (k), and if k is small in comparison to n, then we can take log (p) » n*log(2). Then the expected number of tests required on numbers surviving a sieve to q (rounding up to nearest integer) is :

URL : www.glasgowg43.freeserve.co.uk/survive.htm